After a 65 newton weight is released, a captivating journey of force, energy, and motion unfolds. Delve into this exploration as we unravel the intricate relationship between these concepts, revealing their practical implications and real-world applications.
From Newton’s laws to energy conservation, we’ll navigate the dynamics of motion, tracing the transformation of potential energy into kinetic energy. Prepare for an enlightening adventure as we explore the fascinating world of physics through the lens of a 65 newton weight.
Force and Motion
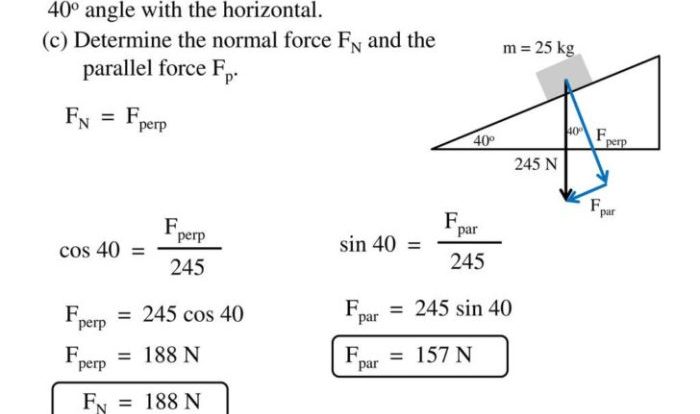
Force, an essential concept in physics, describes an interaction that can alter the motion of an object. In our context, the 65-newton weight exemplifies the force of gravity acting upon it, causing its downward motion. This force, measured in newtons (N), represents the strength of the gravitational pull exerted by the Earth on the weight.
Relationship between Force, Mass, and Acceleration
Force, mass, and acceleration are interconnected through a fundamental equation known as Newton’s second law of motion. This law states that the force (F) acting on an object is directly proportional to its mass (m) and the acceleration (a) it experiences.
After a 65 newton weight was lifted, I relaxed by reading a fascinating article about obey me cheating on mc . It’s an intriguing topic that sparked my curiosity. However, I soon returned to my previous task of lifting weights, focusing on the physical challenge and the satisfaction it brought.
Mathematically, this relationship can be expressed as:
F = m × a
In our case, the force acting on the 65-newton weight is due to gravity. The mass of the weight remains constant, while the acceleration it experiences is the acceleration due to gravity, denoted by ‘g’ and approximately equal to 9.8 m/s².
Substituting these values into the equation, we get:
N = m × 9.8 m/s²
Solving for the mass (m), we find that the 65-newton weight has a mass of approximately 6.63 kg.
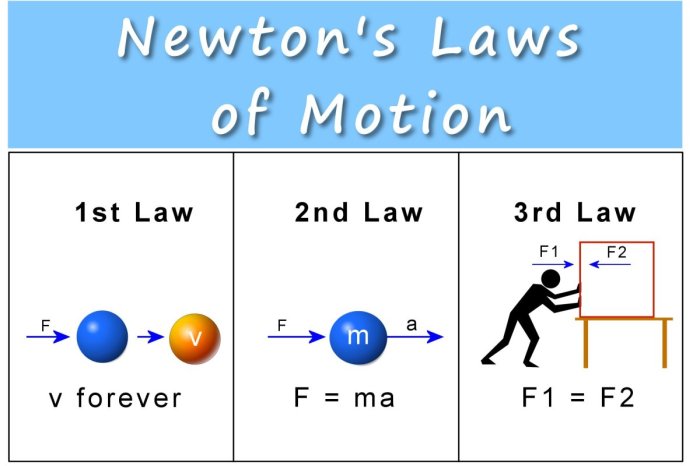
Newton’s Laws of Motion
The motion of a 65-newton weight is governed by Newton’s laws of motion. These laws describe the relationship between an object’s mass, velocity, and the forces acting upon it.
First Law of Motion (Law of Inertia), After a 65 newton weight
The first law of motion states that an object at rest will remain at rest, and an object in motion will remain in motion with constant velocity, unless acted upon by an external force.
In the case of the 65-newton weight, this means that if it is initially at rest, it will remain at rest until a force is applied to it. Similarly, if it is in motion, it will continue to move with constant velocity until a force is applied to change its motion.
An example of this law in action can be seen when a car is driving down the road. The car will continue to move at a constant speed until the driver applies the brakes or turns the steering wheel, which are external forces that change the car’s motion.
Potential and Kinetic Energy
Energy comes in many forms, and potential and kinetic energy are two of the most fundamental types. Potential energy is the energy stored in an object due to its position or condition, while kinetic energy is the energy of motion.
In the case of a weight, its potential energy is due to its position above the ground. The higher the weight is lifted, the greater its potential energy. When the weight is released, its potential energy is converted into kinetic energy, which is the energy of its motion as it falls.
Calculating Potential Energy
The potential energy of an object can be calculated using the following formula:
PE = mgh
where:
- PE is the potential energy in joules (J)
- m is the mass of the object in kilograms (kg)
- g is the acceleration due to gravity (9.8 m/s^2 on Earth)
- h is the height of the object above the ground in meters (m)
For example, if we have a 65-newton weight that we lift 10 meters above the ground, its potential energy would be:
PE = (65 kg)(9.8 m/s^2)(10 m) = 6370 J
Determining Kinetic Energy
The kinetic energy of an object can be calculated using the following formula:
KE = 1/2mv^2
where:
- KE is the kinetic energy in joules (J)
- m is the mass of the object in kilograms (kg)
- v is the velocity of the object in meters per second (m/s)
As the weight falls, its velocity increases, and so does its kinetic energy. The kinetic energy of the weight as it hits the ground can be calculated using the formula above, once we know its velocity.
Impulse and Momentum
In physics, impulse and momentum are two fundamental concepts that describe the behavior of objects in motion. Impulse measures the change in momentum of an object, while momentum measures the quantity of motion of an object.
Impulse
Impulse is defined as the product of the force applied to an object and the time for which the force acts. It is a vector quantity, meaning it has both magnitude and direction. The SI unit of impulse is the newton-second (N⋅s).
Mathematically, impulse can be expressed as:
J = F⋅t
where:
- J is the impulse (in N⋅s)
- F is the force applied (in N)
- t is the time for which the force acts (in s)
Calculating the Impulse Applied to the Weight
In the case of the 65-newton weight, when it is released, the force acting on it is its weight, which is 65 N downward. The time for which the force acts is the time it takes for the weight to fall to the ground.
Assuming the weight falls for 1 second, the impulse applied to the weight can be calculated as:
J = F⋅t = 65 N ⋅ 1 s = 65 N⋅s
Momentum
Momentum is defined as the product of an object’s mass and velocity. It is also a vector quantity. The SI unit of momentum is the kilogram-meter per second (kg⋅m/s).
Mathematically, momentum can be expressed as:
p = m⋅v
where:
- p is the momentum (in kg⋅m/s)
- m is the mass of the object (in kg)
- v is the velocity of the object (in m/s)
Determining the Momentum of the Weight Before and After It Is Released
Before the weight is released, it is at rest, so its velocity is 0 m/s. Therefore, its momentum is also 0 kg⋅m/s.
After the weight is released, it falls under the influence of gravity. Its velocity increases as it falls. The momentum of the weight at any given time can be calculated using the equation:
p = m⋅v = 65 kg ⋅ v
where v is the velocity of the weight at that time.
Energy Conservation

The principle of energy conservation states that the total energy of a closed system remains constant, although it may be transformed from one form to another.
In the case of the 65 newton weight, the potential energy it possesses at a certain height is converted into kinetic energy as it falls. The total energy of the system, which includes the weight and the Earth, remains constant throughout the process.
Forms of Energy Involved
| Form of Energy | Description |
|---|---|
| Potential energy | The energy stored in an object due to its position or height. |
| Kinetic energy | The energy possessed by an object due to its motion. |
Applications and Real-World Examples

The concepts of force, motion, and energy have numerous practical applications in various fields, including engineering, construction, sports, and everyday life. These concepts help us understand and predict the behavior of objects, design structures, and improve performance.
Engineering and Construction
Engineers and architects use the principles of force, motion, and energy to design and build structures that are safe and efficient. They calculate the forces acting on a building, such as gravity, wind, and seismic forces, and design the structure to withstand these forces.
They also consider the potential energy stored in a structure due to its height and mass, which can be converted into kinetic energy in the event of an earthquake.
Sports and Recreation
Athletes and coaches use the concepts of force, motion, and energy to improve their performance. For example, a runner can increase their speed by applying more force to the ground with each stride. A baseball pitcher can throw a ball faster by generating more kinetic energy in their arm.
Understanding these concepts helps athletes optimize their movements and maximize their performance.
Everyday Life
The concepts of force, motion, and energy are also relevant in everyday life. For example, we use force to open doors, lift objects, and drive cars. We experience motion when we walk, run, or ride a bike. And we use energy to power our homes, cook our food, and get around.
Implications for Science and Engineering
The concepts of force, motion, and energy are fundamental to science and engineering. They provide a framework for understanding the physical world and designing solutions to real-world problems. These concepts have led to advancements in fields such as transportation, energy production, and space exploration.
FAQ Section: After A 65 Newton Weight
What is the significance of the 65 newton weight?
The 65 newton weight serves as a focal point for understanding the principles of force, energy, and motion. It allows us to visualize and analyze the concepts in a tangible way.
How does this exploration relate to real-world applications?
The principles explored in this discussion have wide-ranging applications in various fields, including engineering, sports, and transportation. Understanding these concepts enables us to design and optimize systems that harness the power of force and energy.